 18.3 Modern Dating Methods
18.3 Modern Dating Methods
Radiometric dating has been carried out since 1905, and since then the techniques have been greatly improved and expanded. Dating can now be performed on samples as small as a billionth of a gram using a mass spectrometer. The mass spectrometer operates by generating a beam of ionized atoms from the sample under test. The ions then travel through a magnetic field, which diverts them into different sampling sensors, known as “Faraday cups“, depending on their mass and level of ionization. On impact in the cups, the ions set up a very weak current that can be measured to determine the rate of impacts and the relative concentrations of different atoms in the beams.
18.3.1 Uranium-Lead Dating Method
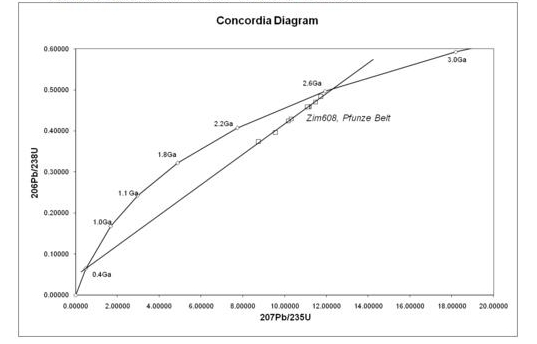
A Concordia diagram as used in uranium-lead dating, with data from the Pfunze Belt, Zimbabwe. All the samples show loss of lead isotopes, but the intercept of the errorchron (straight line through the sample points) and the Concordia (curve) shows the correct age of the rock.
The uranium-lead radiometric dating scheme has been refined to the point that the error margin in dates of rocks can be as low as two million years in two-and-a-half billion year rocks. An error margin of 2–5 % has been achieved on younger Mesozoic rocks.
One of its great advantages is that any sample provides two clocks, one based on uranium-235’s decay to lead-207 with a half-life of about 700 million years, and one based on uranium-238’s decay to lead-206 with a half-life of about 4.5 billion years, providing a built-in cross-check that allows accurate determination of the age of the sample even if some of the lead has been lost.
18.3.2 Samarium-Neodymium Dating Method
This involves the alpha-decay of 147Sm to 143Nd with a half life of 1.06 x 1011 years. Accuracy levels of less than twenty million years in two-and-a-half billion years are achievable.
18.3.3 Potassium-Argon Dating Method
This involves electron capture or positron decay of potassium-40 to argon-40. Potassium-40 has a half-life of 1.3 billion years, and so this method is applicable to the oldest rocks.
18.3.4 Rubidium-Strontium Dating Method
This is based on the beta decay of rubidium-87 to strontium-87, with a half-life of 50 billion years. This scheme is used to date old igneous and metamorphic rocks, and has also been used to date lunar samples. Closure temperatures are so high that they are not a concern. Rubidium-strontium dating is not as precise as the uranium-lead method, with errors of 30 to 50 million years for a 3-billion-year-old sample.
18.3.5 Uranium-Thorium Dating Method
A relatively short-range dating technique is based on the decay of uranium-238 into thorium-230, a substance with a half-life of about 80,000 years. It is accompanied by a sister process, in which uranium-235 decays into protactinium-231, which has a half-life of 34,300 years.
While uranium is water-soluble, thorium and protactinium are not, and so they are selectively precipitated into ocean-floor sediments, from which their ratios are measured. The scheme has a range of several hundred thousand years.
18.3.6 Radiocarbon Dating Method
Radiocarbon dating, or carbon dating, is a radiometric dating method that uses the naturally occurring radioisotope carbon-14 (14C) to determine the age of carbonaceous materials up to about 60,000 years.
Carbon-14 is a radioactive isotope of carbon, with a half-life of 5,730 years, which is very short compared with those above. The parent isotopes have been decaying since they were formed in the stars, and so any parent isotope with a short half-life should be extinct by now. Carbon–14 is an exception. It is continuously created through collisions of neutrons generated by cosmic rays with nitrogen in the upper atmosphere. The carbon-14 ends up as a trace component in atmospheric carbon dioxide (CO2).
Organisms acquire carbon during their lifetime. Plants acquire it through photosynthesis, and animals acquire it from consumption of plants and other animals. When an organism dies, it ceases to take in new carbon-14, and the existing isotope decays with its characteristic half-life (5730 years). The proportion of carbon-14 left when the remains of the organism are examined provides an indication of the time elapsed since its death. The carbon–14 dating limits lie around 58,000 to 62,000 years.
The rate of creation of carbon-14 appears to be roughly constant, as cross-checks of carbon–14 dating with other dating methods show. However, local eruptions of volcanoes or other events that give off large amounts of carbon dioxide can reduce local concentrations of carbon–14 and give inaccurate dates.
One of the most frequent uses of radiocarbon dating is to estimate the age of organic remains from archaeological sites. When plants fix atmospheric carbon dioxide (CO2) into organic material during photosynthesis they incorporate a quantity of 14C that approximately matches the level of this isotope in the atmosphere. After plants die, or after they are consumed by other organisms, the 14C fraction of this organic material declines at a fixed exponential rate due to the radioactive decay of 14C. Comparing the remaining 14C fraction of a sample to that expected from atmospheric 14C allows the age of the sample to be estimated.
The technique of radiocarbon dating was developed by Willard Libby and his colleagues at the University of Chicago in 1949. He first demonstrated the accuracy of radiocarbon dating by accurately measuring the age of wood from an ancient Egyptian royal barge whose age was known from historical documents.
a- Basic Physics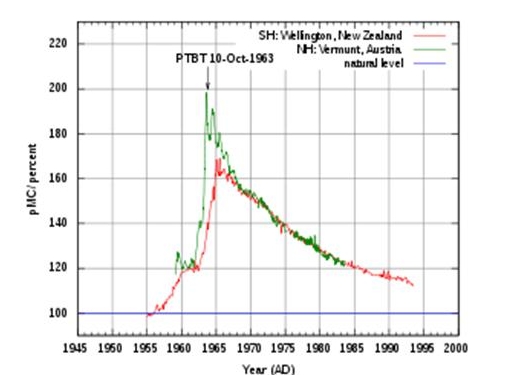
Atmospheric 14C, New Zealand and Austria. The New Zealand curve is representative for the Southern Hemisphere, the Austrian curve is representative for the Northern Hemisphere. Atmospheric nuclear weapon tests almost doubled the concentration of 14C in the Northern Hemisphere.
Carbon has two stable, non-radioactive isotopes: carbon-12 (12C), and carbon-13 (13C). In addition, there are trace amounts of the unstable isotope carbon-14 (14C) on Earth. Carbon-14 has a half-life of 5730 years and would have long ago vanished from Earth were it not for the unremitting cosmic ray impacts on nitrogen in the Earth’s atmosphere, which create more of the isotope. The neutrons resulting from the cosmic ray interactions participate in the following nuclear reaction on the atoms of nitrogen molecules (N2) in the atmosphere:
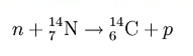
The highest rate of carbon-14 production takes place at altitudes of 9 to 15 km, and at high geomagnetic latitudes, but the carbon-14 spreads evenly throughout the atmosphere and reacts with oxygen to form carbon dioxide. Carbon dioxide also permeates the oceans, dissolving in the water. For approximate analysis it is assumed that the cosmic ray flux is constant over long periods of time; thus carbon-14 is produced at a constant rate and the proportion of radioactive to non-radioactive carbon is constant: ca. 1 part per trillion (600 billion atoms/mole). For the most accurate work, local variations are compensated by means of calibration curves.
Plants take up atmospheric carbon dioxide by photosynthesis, and are ingested by animals, so every living thing is constantly exchanging carbon-14 with its environment as long as it lives. Once it dies, however, this exchange stops, and the amount of carbon-14 gradually decreases through radioactive beta decay with a half-life of 5,730±40 years.
![]()
Carbon-14, 14C, or radiocarbon, is a radioactive isotope of carbon. Its nucleus contains 6 protons and 8 neutrons. Its presence in organic materials is the basis of the radiocarbon dating method to date archaeological, geological, and hydro-geological samples.
b- Computation of Ages and Dates
The radioactive decay of carbon-14 follows an exponential decay. Symbolically, this can be expressed as the following differential equation, where N is the quantity and λ is a positive number called the decay constant:
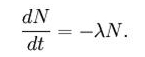
The solution to this equation is:
![]()
where, for a given sample of carbonaceous matter:
N0 = number of radiocarbon atoms at t = 0, i.e. the origin of the disintegration time,
N = number of radiocarbon atoms remaining after radioactive decay during the time t,
λ = radiocarbon decay or disintegration constant.
Two related times can be defined:
• mean- or average-life: mean or average time each radiocarbon atom spends in a given sample until it decays.
• half-life: time lapsed for half the number of radiocarbon atoms in a given sample, to decay,
It can be shown that:

Notice that dates are customarily given in years BP which implies t(BP) = -t because the time arrow for dates runs in reverse direction from the time arrow for the corresponding ages. From these considerations and the above equation, it results:
– for a raw radiocarbon date:

– and for a raw radiocarbon age:
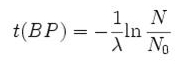
After replacing values, the raw radiocarbon age becomes any of the following equivalent formulae:
– using logs base e and the average life:

– and using logs base 2 and the half-life:

Wiggle matching uses the non-linear relationship between the 14C age and calendar age to match the shape of a series of closely sequentially spaced 14C dates with the 14C calibration curve.
c- Measurements and Scales
Measurements are made by counting the radioactive decay of individual carbon atoms by gas proportional counting, or by liquid scintillation counting. For samples of sufficient size (several grams of carbon) this method is still widely used in the 2000s. Among others, all the tree ring samples used for the calibration curves were determined by these counting techniques. Such decay counting, however, is relatively insensitive and subject to large statistical uncertainties for small samples. When there is little carbon-14 to begin with, the long radiocarbon half-life means that very few of the carbon-14 atoms will decay during the time allotted for their detection, resulting in few disintegrations per minute.
The sensitivity of the method has been greatly increased by the use of Accelerator Mass Spectrometry (AMS). With this technique 14C atoms can be detected and counted directly versus only detecting those atoms that decay during the time interval allotted for an analysis. AMS allows dating samples containing only a few milligrams of carbon.
Radiocarbon dating laboratories generally report an uncertainty for each date. For example, 3000±30BP indicates a standard deviation of 30 radiocarbon years. Traditionally this included only the statistical counting uncertainty. However, some laboratories supplied an “error multiplier” that could be multiplied by the uncertainty to account for other sources of error in the measuring process. More recently, the laboratories try to quote the overall uncertainty, which is determined from control samples of known age and verified by international inter-comparison exercises. In 2008, a typical uncertainty better than ±40 radiocarbon years can be expected for samples younger than 10,000 years.
As of 2007, the limiting age for a 1 milligram sample of graphite is about ten half-lives, approximately 60,000 years. This age is derived from that of the calibration blanks used in an analysis, whose 14C content is assumed to be the result of contamination during processing.
d- The Need for Calibration
Calibration curve for the radiocarbon dating scale. Data sources: Stuiver et al. (1998). Samples with a real date more recent than AD 1950 are dated and/or tracked using the N- & S-Hemisphere graphs. See preceding figure.
A raw BP date cannot be used directly as a calendar date, because the level of atmospheric 14C has not been strictly constant during the span of time that can be radiocarbon dated. The level is affected by variations in the cosmic ray intensity which is in turn affected by variations in the earth’s magnetosphere. In addition, there are substantial reservoirs of carbon in organic matter, the ocean, ocean sediments, and sedimentary rocks. Changes in the Earth’s climate can affect the carbon flows between these reservoirs and the atmosphere, leading to changes in the atmosphere’s 14C fraction.
Aside from these changes due to natural processes, the level has also been affected by human activities. From the beginning of the industrial revolution in the 18th century to the 1950s, the fractional level of 14C decreased because of the admixture of large quantities of CO2 into the atmosphere, due to the excavated oil reserves and combustion production of fossil fuel. Atmospheric 14C was almost doubled for a short period during the 1950s and 1960s due to atmospheric atomic bomb tests.
As a consequence, the radiocarbon method shows limitations on dating of materials that are younger than the industrialization. Due to the drastical fluctuations, higher carbon-14 content does not always mean young age.
e- Calibration Methods
The raw radiocarbon dates, in BP years, are calibrated to give calendar dates. Standard calibration curves are available, based on comparison of radiocarbon dates of samples that can be dated independently by other methods such as examination of tree growth rings (dendrochronology), deep ocean sediment cores, lake sediment varves, coral samples, and speleothems (cave deposits).
The calibration curves can vary significantly from a straight line, so comparison of uncalibrated radiocarbon dates is likely to give misleading results. There are also significant plateaus in the curves, such as the one from 11,000 to 10,000 radiocarbon years BP, which is believed to be associated with changing ocean circulation during the Younger Dryas period. Over the historical period from 0 to 10,000 years BP, the average width of the uncertainty of calibrated dates was found to be 335 years, although in well-behaved regions of the calibration curve the width decreased to about 113 years while in ill-behaved regions it increased to a maximum of 801 years.
f- Radiocarbon Half-Life
Carbon dating was developed by a team led by Willard Libby. He worked out a carbon-14 half-life of 5568±30 years, the Libby half-life. Later a more accurate figure of 5730±40 years was determined, which is known as the Cambridge half-life. This is, however, not relevant for radiocarbon dating. If calibration is applied, the half-life cancels out. Laboratories continue to use the Libby figure to avoid inconsistencies with previous publications.
g- Carbon Exchange Reservoir
Libby’s original exchange reservoir hypothesis assumes that the exchange reservoir is constant all over the world. The calibration method also assumes that the temporal variation in 14C level is global. However, since Libby’s early work was published (1950 to 1958), latitudinal and continental variations in the carbon exchange reservoir have been observed. Subsequently, methods have been developed that allow the correction of these so-called reservoir effects, including:
• When CO2 is transferred from the atmosphere to the oceans, it initially shares the 14C concentration of the atmosphere. However, turnaround times of CO2 in the ocean are similar to the half-life of 14C. Marine organisms feed on this “old” carbon, and thus their radiocarbon age reflects the time of CO2 uptake by the ocean rather than the time of death of the organism.
• Erosion and immersion of carbonate rocks (which are generally older than 80,000 years and so shouldn’t contain measurable 14C) causes an increase in 12C and 13C in the exchange reservoir, which depends on local weather conditions and can vary the ratio of carbon that living organisms incorporate. This is believed negligible for the atmosphere and atmosphere-derived carbon since most erosion will flow into the sea.
• Volcanic eruptions eject large amount of carbonate into the air, causing an increase in 12C and 13C in the exchange reservoir and can vary the exchange ratio locally. This explains the often irregular dating achieved in volcanic areas.
• The earth is not affected evenly by cosmic radiation as the magnitude of the radiation depends on land altitude and earth’s magnetic field strength at any given location, causing minor variation in the local 14C production. This is accounted for by having calibration curves for different locations of the globe.
These effects were first confirmed when samples of wood from around the world, which all had the same age (based on tree ring analysis), showed deviations from the dendrochronological age. Calibration techniques based on tree-ring samples have contributed to increase the accuracy since 1962, when they were accurate to 700 years at worst.
18.3.7 Fission Track Dating Method
This involves inspection of a polished slice of a material to determine the density of “track” markings left in it by the spontaneous fission of uranium-238 impurities. The uranium content of the sample has to be known, but that can be determined by placing a plastic film over the polished slice of the material, and bombarding it with slow neutrons. This causes induced fission of 235U, as opposed to the spontaneous fission of 238U. The fission tracks produced by this process are recorded in the plastic film. The uranium content of the material can then be calculated from the number of tracks and the neutron flux.
This scheme has application over a wide range of geologic dates. For dates up to a few million years micas, tektites, and meteorites are best used. Older materials can be dated using zircon, apatite, titanite, epidote and garnet which have a variable amount of uranium content. Because the fission tracks are healed by temperatures over about 200°C the technique has limitations as well as benefits.
18.3.8 Chlorine-36 Dating Method
Large amounts of otherwise rare 36Cl were produced by irradiation of seawater during atmospheric detonations of nuclear weapons between 1952 and 1958. The residence time of 36Cl in the atmosphere is about 1 week. Thus, as an event marker of 1950s water in soil and ground water, 36Cl is also useful for dating waters less than 50 years before the present.
18.3.9 Optically Stimulated Luminescence Dating Method
Natural sources of radiation in the environment knock loose electrons in, say, a piece of pottery, and these electrons accumulate in defects in the material’s crystal lattice structure. Heating the object will release the captured electrons, producing a luminescence. When the sample is heated, at a certain temperature it will glow from the emission of electrons released from the defects, and this glow can be used to estimate the age of the sample to a threshold of approximately 15 percent of its true age. The date of a rock is reset when volcanic activity remelts it. The date of a piece of pottery is reset by the heat of the kiln. Typically temperatures greater than 400 degrees Celsius will reset the “clock”. This is termed thermoluminescence.
