The age of the universe is the time elapsed between the Big Bang and the present day. Current theory and observations suggest that this is between 13.5 and 14 billion years. The uncertainty range has been obtained by the agreement of a number of scientific research projects. Scientific instruments and methods have improved the ability to measure the age of the universe with a great accuracy. Background radiation measurements give the cooling time of the universe since the big bang. Expansion of the universe measurements give accurate data to calculate the age of the universe.
19.4.1 Explanation
The Lambda-CDM concordance model describes the evolution of the universe from a very uniform, hot, dense primordial state to its present state over a span of about 13.75 billion years of cosmological time. However theories of the origin of the primordial state remain very speculative. If one extrapolates the Lambda-CDM model backward from the earliest well-understood state, it quickly reaches a singularity called the “Big Bang singularity.”
Though the universe might in theory have a longer history, cosmologists presently use “age of the universe” to mean the duration of the Lambda-CDM expansion, or equivalently, the elapsed time since the Big Bang.
19.4.2 Observational Limits
The universe must be at least as old as the oldest thing in it; there are a number of observations which put a lower limit on the age of the universe. These include the temperature of the coolest white dwarfs, and the turnoff point of the red dwarfs. On April 23, 2009 a gamma-ray burst was detected which was later confirmed at being over 13 billion years old.
19.4.3 Cosmological Parameters
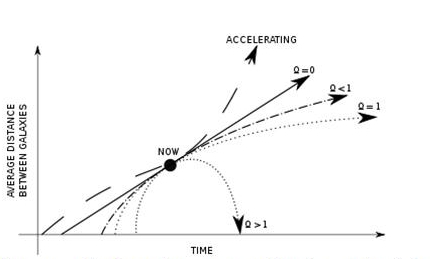
The age of the universe can be determined by measuring the Hubble constant today and extrapolating back in time with the observed value of density parameters (Ω). Before the discovery of dark energy, it was believed that the universe was matter-dominated, and so Ω on this graph corresponds to Ωm. Note that the accelerating universe has the greatest age, while the Big Crunch universe has the smallest age.

The value of the age correction factor F is shown as a function of two cosmological parameters: the current fractional matter density Ωm and cosmological constant density ΩΛ. The best-fit values of these parameters are shown by the box in the upper left; the matter-dominated universe is shown by the star in the lower right.
The problem of determining the age of the universe is closely tied to the problem of determining the values of the cosmological parameters. Today this is largely carried out in the context of the ΛCDM model, where the Universe is assumed to contain normal (baryonic) matter, cold dark matter, radiation (including both photons and neutrinos), and a cosmological constant. The fractional contribution of each to the current energy density of the Universe is given by the density parameters Ωm, Ωr, and ΩΛ. The full ΛCDM model is described by a number of other parameters, but for the purpose of computing its age these three, along with the Hubble parameter H0 are the most important.
If one has accurate measurements of these parameters, then the age of the universe can be determined by using the Friedmann equation. This equation relates the rate of change in the scale factor a(t) to the matter content of the Universe. Turning this relation around, we can calculate the change in time per change in scale factor and thus calculate the total age of the universe by integrating this formula.
The age t0 is then given by an expression of the form:
![]()
where the function F depends only on the fractional contribution to the universe’s energy content that comes from various components. The first observation that one can make from this formula is that it is the Hubble parameter that controls that age of the universe, with a correction arising from the matter and energy content. So a rough estimate of the age of the universe comes from the inverse of the Hubble parameter,

To get a more accurate number, the correction factor F must be computed. In general this must be done numerically, and the results for a range of cosmological parameter values are shown in the figure. For the WMAP values (Ωm, ΩΛ) = (0.266, 0.732), shown by the box in the upper left corner of the figure, this correction factor is nearly one: F = 0.996. For a flat universe without any cosmological constant, shown by the star in the lower right corner, F = 2/3 is much smaller and thus the universe is younger for a fixed value of the Hubble parameter. To make this figure, Ωr is held constant (roughly equivalent to holding the CMB temperature constant) and the curvature density parameter is fixed by the value of the other three.
The cosmological constant makes the universe “older” for fixed values of the other parameters. This is significant, since before the cosmological constant became generally accepted, the Big Bang model had difficulty explaining why globular clusters in the Milky Way appeared to be far older than the age of the universe as calculated from the Hubble parameter and a matter-only universe. Introducing the cosmological constant allows the universe to be older than these clusters, as well as explaining other features that the matter-only cosmological model could not.
19.4.5 WMAP
NASA’s Wilkinson Microwave Anisotropy Probe (WMAP) project estimates the age of the universe to be:
(1.373 ± 0.012) × 1010 years.
That is, the universe is about 13.73 billion years old, with an uncertainty of 120 million years.
19.4.6 Assumption of Strong Priors
Calculating the age of the universe is only accurate if the assumptions built into the models being used to estimate it are also accurate. This is referred to as strong priors.
The age of the universe based on the “best fit” to WMAP data “only” is 13.69±0.13 Gyr (the slightly higher number of 13.73 includes some other data mixed in). This number represents the first accurate “direct” measurement of the age of the universe.


Be First to Comment